Что называется угловым коэффициентом прямой. Угловой коэффициент касательной как тангенс угла наклона

Численно равен тангенсу угла (составляющего наименьший поворот от оси Ox к оси Оу) между положительным направлением оси абсцисс и данной прямой линией.

Тангенс угла может рассчитываться как отношение противолежащего катета к прилежащему. k всегда равен , то есть производной уравнения прямой по x .

При положительных значениях углового коэффициента k и нулевом значении коэффициента сдвига b прямая будет лежать в первом и третьем квадрантах (в которых x и y одновременно положительны и отрицательны). При этом большим значениям углового коэффициента k будет соответствовать более крутая прямая, а меньшим - более пологая.

Прямые и перпендикулярны, если , а параллельны при .

Примечания

Wikimedia Foundation . 2010 .

• Ифит (царь Элиды)
• Список Указов Президента РФ «О награждении государственными наградами» за 2001 год

Смотреть что такое "Угловой коэффициент прямой" в других словарях:

угловой коэффициент (прямой) - — Тематики нефтегазовая промышленность EN slope … Справочник технического переводчика

Угловой коэффициент - (математическое) число k в уравнении прямой линии на плоскости у = kx+b (см. Аналитическая геометрия), характеризующее наклон прямой относительно оси абсцисс. В прямоугольной системе координат У. к. k = tg φ, где φ угол между… … Большая советская энциклопедия

Уравнения прямой

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ - раздел геометрии, который исследует простейшие геометрические объекты средствами элементарной алгебры на основе метода координат. Создание аналитической геометрии обычно приписывают Р.Декарту, изложившему ее основы в последней главе своего… … Энциклопедия Кольера

Время реакции (reaction time) - Измерение времени реакции (ВР), вероятно, самый почтенный предмет в эмпирической психологии. Оно зародилось в области астрономии, в 1823 г., с измерением индивидуальных различий в скорости восприятия пересечения звездой линии риски телескопа. Эти … Психологическая энциклопедия

МАТЕМАТИЧЕСКИЙ АНАЛИЗ - раздел математики, дающий методы количественного исследования разных процессов изменения; занимается изучением скорости изменения (дифференциальное исчисление) и определением длин кривых, площадей и объемов фигур, ограниченных кривыми контурами и … Энциклопедия Кольера

Прямая - У этого термина существуют и другие значения, см. Прямая (значения). Прямая одно из основных понятий геометрии, то есть точного универсального определения не имеет. При систематическом изложении геометрии прямая линия обычно принимается за одно… … Википедия

Прямая линия - Изображение прямых в прямоугольной системе координат Прямая одно из основных понятий геометрии. При систематическом изложении геометрии прямая линия обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется… … Википедия

Прямые - Изображение прямых в прямоугольной системе координат Прямая одно из основных понятий геометрии. При систематическом изложении геометрии прямая линия обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется… … Википедия

Малая полуось - Не следует путать с термином «Эллипсис». Эллипс и его фокусы Эллипс (др. греч. ἔλλειψις недостаток, в смысле недостатка эксцентриситета до 1) геометрическое место точек M Евклидовой плоскости, для которых сумма расстояний от двух данных точек F1… … Википедия

Пусть на плоскости, где имеется прямоугольная декартова система координат, прямая l проходит через точку М 0 параллельно направляющему вектору а (рис. 96).

Если прямая l пересекает ось Ох (в точке N), то под углом прямой l с осью Ох будем понимать угол α, на который необходимо повернуть ось Ох вокруг точки N в направлении, обратном вращению часовой стрелки, чтобы ось Ох совпала с прямой l . (Имеется в виду угол, меньший 180°.)

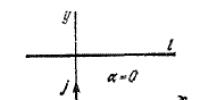
Этот угол называют углом наклона прямой. Если прямая l параллельна оси Ох , то угол наклона принимается равным нулю (рис. 97).

Тангенс угла наклона прямой называется угловым коэффициентом прямой и обычно обозначается буквой k :

tg α = k . (1)

Если α = 0, то и k = 0; это означает, что прямая параллельна оси Ох и ее угловой коэффициент равен нулю.

Если α = 90°, то k = tg α не имеет смысла: это означает, что прямая, перпендикулярная оси Ох (т. е. параллельная оси Оу ), не имеет углового коэффициента.

Угловой коэффициент прямой можно вычислить, если известны координаты двух каких-либо точек этой прямой. Пусть даны две точки прямой: M 1 (x 1 ; у 1) и M 2 (x 2 ; у 2) и пусть, например, 0 < α < 90°, а x 2 > x 1 , у 2 > у 1 (рис. 98).

Тогда из прямоугольного треугольника M 1 РM 2 находим

$$ k=tga = \frac{|M_2 P|}{|M_1 P|} = \frac{y_2 - y_1}{x_2 - x_1} $$

$$ k=\frac{y_2 - y_1}{x_2 - x_1} \;\; (2)$$

Аналогично доказывается, что формула (2) верна и в случае 90° < α < 180°.

Формула (2) теряет смысл, если x 2 - x 1 = 0, т. е. если прямая l параллельна оси Оу . Для таких прямых угловой коэффициент не существует.

Задача 1. Определить угловой коэффициент примой, проходящей через точки

M 1 (3; -5) и М 2 (5; -7).

Подставляя координаты точек M 1 и М 2 в формулу (2), получим

\(k=\frac{-7-(-5)}{5-3} \) или k = -1

Задача 2. Определить угловой коэффициент прямой, проходящей через точки M 1 (3; 5) и M 2 (3; -2).

Так как x 2 - x 1 = 0, то равенство (2) теряет смысл. Для этой прямой угловой коэффициент не существует. Прямая M 1 M 2 параллельна оси Оу .

Задача 3. Определить угловой коэффициент прямой, проходящей через начало координат и точку M 1 (3; -5)

В этом случае точка M 2 совпадает с началом координат. Применяя формулу (2), получим

$$ k=\frac{y_2 - y_1}{x_2 - x_1}=\frac{0-(-5)}{0-3}= -\frac{5}{3}; \;\; k= -\frac{5}{3} $$

Составим уравнение прямой с угловым коэффициентом k , проходящей через точку

M 1 (x 1 ; у 1). По формуле (2) угловой коэффициент прямой находится по координатам двух ее точек. В нашем случае точка M 1 задана, а в качестве второй точки можно взять любую точку М(х; у ) искомой прямой.

Если точка М лежит на прямой, которая проходит через точку M 1 и имеет угловой коэффициент k , то в силу формулы (2) имеем

$$ \frac{y-y_1}{x-x_1}=k \;\; (3) $$

Если же точка М не лежит на прямой, то равенство (3) не выполняется. Следовательно, равенствo (3) и есть уравнение прямой, проходящей через точку M 1 (x 1 ; у 1) с угловым коэффициентом k ; это уравнение обычно записывают в виде

y - y 1 = k (x - x 1). (4)

Если прямая пересекает ось Оу в некоторой точке (0; b ), то уравнение (4) принимает вид

у - b = k (х - 0),

y = kx + b . (5)

Это уравнение называется уравнением прямой с угловым коэффициентом k и начальной ординатой b.

Задача 4. Найти угол наклона прямой √3 х + 3у - 7 = 0.

Приведем данное уравнение к виду

$$ y= =\frac{1}{\sqrt3}x + \frac{7}{3} $$

Следовательно, k = tg α = - 1 / √ 3 , откуда α = 150°

Задача 5. Составить уравнение прямой, проходящей через точку Р(3; -4), с угловым коэффициентом k = 2 / 5

Подставив k = 2 / 5 , x 1 = 3, y 1 = - 4 в уравнение (4), получим

у - (- 4) = 2 / 5 (х - 3) или 2х - 5у - 26 = 0.

Задача 6. Составить уравнение прямой, проходящей через точку Q (-3; 4) и составляющей с положительным направлением оси Ох угол 30°.

Если α = 30°, то k = tg 30° = √ 3 / 3 . Подставив в уравнение (4) значения x 1 , y 1 и k , получим

у -4 = √ 3 / 3 (x + 3) или √3 x -3y + 12 + 3√3 = 0.

Задачи на нахождение производной касательной включены в ЕГЭ по математике и встречаются там ежегодно. При этом статистика последних лет показывает, что подобные задания вызывают у выпускников определенные затруднения. Поэтому, если учащийся рассчитывает получить достойные баллы по итогам прохождения ЕГЭ, то ему непременно стоит научиться справляться с задачами из раздела «Угловой коэффициент касательной как значение производной в точке касания», подготовленными специалистами образовательного портала «Школково». Разобравшись с алгоритмом их решения, ученик сможет успешно преодолеть аттестационное испытание.

Основные моменты

Приступая к решению задач ЕГЭ по данной теме, необходимо вспомнить основное определение: производная функции в точке равна угловому коэффициенту касательной к графику функции в этой точке. В этом и состоит геометрический смысл производной.

Необходимо освежить в памяти и другое важное определение. Оно звучит следующим образом: угловой коэффициент равняется тангенсу угла наклона касательной к оси абсцисс.

Какие еще важные моменты стоит отметить в этой теме? При решении задач на нахождение производной в ЕГЭ необходимо помнить, что угол, который образует касательная, может быть меньше, больше 90 градусов или равняться нулю.

Как подготовиться к экзамену?

Для того, чтобы задания в ЕГЭ на тему «Угловой коэффициент касательной как значение производной в точке касания» давались вам достаточно легко, воспользуйтесь при подготовке к выпускному испытанию информацией по этому разделу на образовательном портале «Школково». Здесь вы найдете необходимый теоретический материал, собранный и понятно изложенный нашими специалистами, а также сможете попрактиковаться в выполнении упражнений.

Для каждого задания, например, задач на тему «Угловой коэффициент касательной как тангенс угла наклона» , мы прописали правильный ответ и алгоритм решения. При этом учащиеся могут выполнять упражнения различного уровня сложности в режиме онлайн. В случае необходимости задачу можно сохранить в разделе «Избранное», чтобы потом обсудить ее решение с преподавателем.

На рисунке показан угол наклона прямой и указано значение углового коэффициента при различных вариантах расположения прямой относительно прямоугольной системы координат.

Нахождение углового коэффициента прямой при известном угле наклона к оси Ox не представляет никаких сложностей. Для этого достаточно вспомнить определение углового коэффициента и вычислить тангенс угла наклона.

Пример.

Найдите угловой коэффициент прямой, если угол ее наклона к оси абсцисс равен .

Решение.

По условию . Тогда по определению углового коэффициента прямой вычисляем .

Ответ:

Задача нахождения угла наклона прямой к оси абсцисс при известном угловом коэффициенте немного сложнее. Здесь необходимо учитывать знак углового коэффициента. При угол наклона прямой является острым и находится как . При угол наклона прямой является тупым и его можно определить по формуле .

Пример.

Определите угол наклона прямой к оси абсцисс, если ее угловой коэффициент равен 3 .

Решение.

Так как по условию угловой коэффициент положителен, то угол наклона прямой к оси Ox острый. Его вычисляем по формуле .

Ответ:

Пример.

Угловой коэффициент прямой равен . Определите угол наклона прямой к оси Ox .

Решение.

Обозначим k – угловой коэффициент прямой, - угол наклона этой прямой к положительному направлению оси Ox . Так как , то используем формулу для нахождения угла наклона прямой следующего вида . Подставляем в нее данные из условия: .

Ответ:

Уравнение прямой с угловым коэффициентом.

Уравнение прямой с угловым коэффициентом имеет вид , где k - угловой коэффициент прямой, b – некоторое действительное число. Уравнением прямой с угловым коэффициентом можно задать любую прямую, не параллельную оси Oy (для прямой параллельно оси ординат угловой коэффициент не определен).

Давайте разберемся со смыслом фразы: «прямая на плоскости в фиксированной системе координат задана уравнением с угловым коэффициентом вида ». Это означает, что уравнению удовлетворяют координаты любой точки прямой и не удовлетворяют координаты никаких других точкек плоскости. Таким образом, если при подстановке координат точки получается верное равенство, то прямая проходит через эту точку. В противном случае точка не лежит на прямой.

Пример.

Прямая задана уравнением с угловым коэффициентом . Принадлежат ли точки и этой прямой?

Решение.

Подставим координаты точки в исходное уравнение прямой с угловым коэффициентом: . Мы получили верное равенство, следовательно, точка М 1 лежит на прямой.

При подстановке координат точки получаем неверное равенство: . Таким образом, точка М 2 не лежит на прямой.

Ответ:

Точка М 1 принадлежит прямой, М 2 – не принадлежит.

Следует отметить, что прямая, определенная уравнением прямой с угловым коэффициентом , проходит через точку , так как при подстановке ее координат в уравнение мы получаем верное равенство: .

Таким образом, уравнение прямой с угловым коэффициентом определяет на плоскости прямую, проходящую через точку и образующую угол с положительным направлением оси абсцисс, причем .

В качестве примера изобразим прямую, определяемую уравнением прямой с угловым коэффициентом вида . Эта прямая проходит через точку и имеет наклон радиан (60 градусов) к положительному направлению оси Ox . Ее угловой коэффициент равен .

Уравнение прямой с угловым коэффициентом, проходящей через заданную точку.

Сейчас решим очень важную задачу: получим уравнение прямой с заданным угловым коэффициентом k и проходящую через точку .

Так как прямая проходит через точку , то справедливо равенство . Число b нам неизвестно. Чтобы избавиться от него, вычтем из левой и правой частей уравнения прямой с угловым коэффициентом соответственно левую и правую части последнего равенства. При этом получим . Это равенство представляет собой уравнение прямой с заданным угловым коэффициентом k , которая проходит через заданную точку .

Рассмотрим пример.

Пример.

Напишите уравнение прямой, проходящей через точку , угловой коэффициент этой прямой равен -2 .

Решение.

Из условия имеем . Тогда уравнение прямой с угловым коэффициентом примет вид .

Ответ:

Пример.

Напишите уравнение прямой, если известно, что она проходит через точку и угол наклона к положительному направлению оси Ox равен .

Решение.

Сначала вычислим угловой коэффициент прямой, уравнение которой мы ищем (такую задачу мы решали в предыдущем пункте этой статьи). По определению . Теперь мы располагаем всеми данными, чтобы записать уравнение прямой с угловым коэффициентом:

Ответ:

Пример.

Напишите уравнение прямой с угловым коэффициентом, проходящую через точку параллельно прямой .

Решение.

Очевидно, что углы наклона параллельных прямых к оси Ox совпадают (при необходимости смотрите статью параллельность прямых), следовательно, угловые коэффициенты у параллельных прямых равны. Тогда угловой коэффициент прямой, уравнение которой нам нужно получить, равен 2 , так как угловой коэффициент прямой равен 2 . Теперь мы можем составить требуемое уравнение прямой с угловым коэффициентом:

Ответ:

Переход от уравнения прямой с угловым коэффициентом к другим видам уравнения прямой и обратно.

При всей привычности уравнение прямой с угловым коэффициентом далеко не всегда удобно использовать при решении задач. В некоторых случаях задачи проще решаются, когда уравнение прямой представлено в другом виде. К примеру, уравнение прямой с угловым коэффициентом не позволяет сразу записать координаты направляющего вектора прямой или координаты нормального вектора прямой . Поэтому следует научиться переходить от уравнения прямой с угловым коэффициентом к другим видам уравнения этой прямой.

Из уравнения прямой с угловым коэффициентом легко получить каноническое уравнение прямой на плоскости вида . Для этого из правой части уравнения переносим слагаемое b в левую часть с противоположным знаком, затем делим обе части полученного равенства на угловой коэффициент k : . Эти действия приводят нас от уравнения прямой с угловым коэффициентом к каноническому уравнению прямой.

Пример.

Приведите уравнение прямой с угловым коэффициентом к каноническому виду.

Решение.

Выполним необходимые преобразования: .

Ответ:

Пример.

Прямая задана уравнением прямой с угловым коэффициентом . Является ли вектор нормальным вектором этой прямой?

Решение.

Для решения этой задачи перейдем от уравнения прямой с угловым коэффициентом к общему уравнению этой прямой: . Нам известно, что коэффициенты перед переменными x и y в общем уравнении прямой являются соответствующими координатами нормального вектора этой прямой, то есть, - нормальный вектор прямой . Очевидно, что вектор коллинеарен вектору , так как справедливо соотношение (при необходимости смотрите статью ). Таким образом, исходный вектор также является нормальным вектором прямой , а, следовательно, является нормальным вектором и исходной прямой .

Ответ:

Да, является.

А сейчас будем решать обратную задачу – задачу приведения уравнения прямой на плоскости к уравнению прямой с угловым коэффициентом.

От общего уравнения прямой вида , в котором , очень легко перейти к уравнению с угловым коэффициентом. Для этого нужно общее уравнение прямой разрешить относительно y . При этом получаем . Полученное равенство представляет собой уравнение прямой с угловым коэффициентом, равным .

В предыдущей главе было показано, что, выбрав определенную систему координат на плоскости, мы можем геометрическое свойства, характеризующее точки рассматриваемой линии, выразить аналитически уравнением между текущими координатами. Таким образом, мы получим уравнение линии. В этой главе будут рассматриваться уравнения прямых линий.

Чтобы составить уравнение прямой в декартовых координатах, нужно каким-то образом задать условия, определяющие положение ее относительно координатных осей.

Предварительно мы введем понятие об угловом коэффициенте прямой, который является одной из величин, характеризующих положение прямой на плоскости.

Назовем углом наклона прямой к оси Ох тот угол, на который нужно повернуть ось Ох, чтобы она совпала с данной прямой (или оказалась параллельной ей). Как обычно, угол будем рассматривать с учетом знака (знак определяется направлением поворота: против или по часовой стрелке). Так как добавочный поворот оси Ох на угол в 180° снова совместит ее с прямой, то угол наклона прямой к оси может быть выбран не однозначно (с точностью до слагаемого, кратного ).

Тангенс этого угла определяется однозначно (так как изменение угла на не меняет его тангенса).

Тангенс угла наклона прямой к оси Ох называется угловым коэффициентом прямой.

Угловой коэффициент характеризует направление прямой (мы здесь не различаем двух взаимно противоположных направлений прямой). Если угловой коэффициент прямой равен нулю, то прямая параллельна оси абсцисс. При положительном угловом коэффициенте угол наклона прямой к оси Ох будет острым (мы рассматриваем здесь наименьшее положительное значение угла наклона) (рис. 39); при этом чем больше угловой коэффициент, тем больше угол ее наклона к оси Ох. Если угловой коэффициент отрицателен, то угол наклона прямой к оси Ох будет тупым (рис. 40). Заметим, что прямая, перпендикулярная к оси Ох, не имеет углового коэффициента (тангенс угла не существует).